9 min to read

유량 그래프 ②:에드몬드-카프 알고리즘

포드-풀커슨 알고리즘의 보완이라 할 수 있는 에드몬드-카프 알고리즘에 대해서 알아봅시다.

Featured image

개요 : 포드-풀커슨 알고리즘의 삽질

우리가 전 글에서 살펴본 포드-풀커슨 알고리즘은, 임의의 유량 그래프가 주어졌을 때, 확실하게 최대 유량을 구할 수 있다는것을 알고 있습니다.

하지만, 포드-풀커슨 알고리즘은 우리가 증가경로를 찾는 방법을 제시하지 않았습니다. 뭔가 싸한 기분이 느껴지지 않나요? 왠지 증가경로를 찾는데에 너무나 많은 시간을 보내게 되어서, 전체 알고리즘의 수행 시간이 느려질것만 같은 그런 기분이?

BFS로 경로를 찾자. 에드몬드-카프 알고리즘

이제 포드-풀커슨 알고리즘이 어떻게 동작하는지와, 그 정당성을 알아보았습니다. 포드-풀커슨 알고리즘은 글의 서두에서도 밝혔듯, 증가경로를 어떻게 찾는지는 별 관심을 두지 않습니다. 그래서, 포드-풀커슨 방법이라고 부르는것이 엄밀히 말하자면 맞는데, 위키백과 표제어에서도 알고리즘이라고 하고, 수많은 인터넷 글에서 알고리즘이라고 하니, 알고리즘으로 불렀습니다.

여하튼 이 점을 언급한 이유는, DFS방식으로 증가경로를 찾는 포드-풀커슨 알고리즘이 비효율 적으로 행동할 수 있는 경우가 있기 때문입니다.

정말로 잘 알려진, 포드-풀커슨 알고리즘이 삽질을 하는 케이스의 그래프를 보여 드리겠습니다.

그림 1 : 포드-풀커슨 알고리즘이 삽질을 할 수 있는 유량 그래프

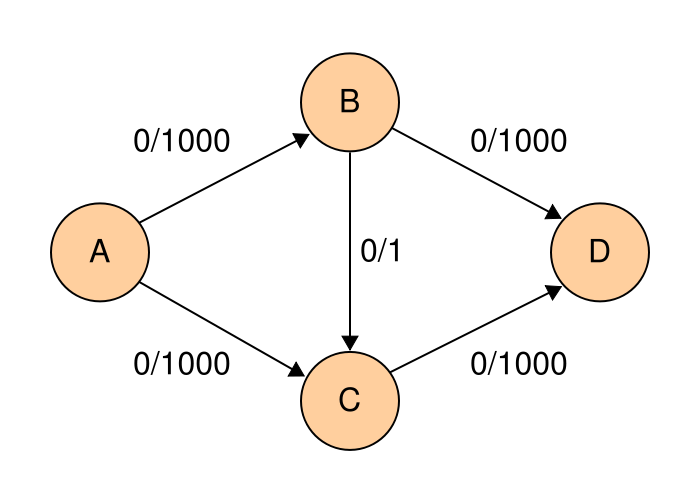
DFS를 이용해서, 유량 그래프의 증가 경로를 찾는다고 하여 봅시다.

총 1000번의 증가경로 탐색이 필요합니다. 하지만, BFS로 증가경로를 찾았다면 어땠을까요?

이걸로 끝입니다. 2번만의 탐색으로 최대 유량을 찾아냈습니다.

포드-풀커슨 알고리즘에서 BFS를 이용하여 증가경로를 찾는 알고리즘을 특별히 에드몬드-카프 알고리즘 이라고 합니다.

에드몬드-카프 알고리즘의 시간복잡도의 증명

에드몬드-카프 알고리즘은, BFS를 쓰지 않는 포드-풀커슨 알고리즘보다 더 빠르게 동작할 것 같다는 생각이 들긴 합니다만, 모든 경우에 대해서 빠르게 동작할것이라는 확신은 들지 않습니다. 그렇기 때문에, 이제 에드몬드-카프 알고리즘의 시간복잡도를 증명함으로써, 이 알고리즘이 실제로 빠른 실행속도를 가지고 있는지 알아보도록 합시다.

에드몬드-카프 알고리즘의 속성을 살펴보면서 증명을 해보도록 합시다.

1. 잔여 그래프 위에서의 거리의 증가성

잔여그래프란, 유량 그래프에서 정점은 그대로되, 간선은 유량을 흘릴 수 있는 간선들만 모아놓은 그래프를 말합니다.

잔여 그래프 위에서의 거리의 증가성은, 증가경로를 찾으면 찾을수록, 잔여 그래프 위에서 임의의 정점에서 종점까지의 거리가 결코 줄지않는다는 것을 증명해봅시다.

즉 이를 일반적으로 나타내면,

임의의 정점 \(v\)에 대해서, 임의의 증가경로를 발견하기 전의 잔여그래프인 \(f\)와, 증가경로를 발견한 후인 \(f'\)에 대해서, 항상 \(d_{f'}(v) \ge d_f(v)\)가 성립한다. \(d(v)\)는 \(v\)에서 종점 \(t\)까지의 거리이다.

이번에 증명은 귀납법을 이용해서 증명해보겠습니다. 임의의 증가경로를 찾기전의 잔여 그래프를 \(G_f\)라고 하고, 그 증가경로를 찾은 이후의 잔여 그래프를 \(G_{f'}\)라고 하여 봅시다. 그리고, \(G_{f'}\)의 정점들을 종점까지의 거리(\(d_{f'}\)라고 하겠습니다)를 기준으로 오름차순 정렬을 하고, 정렬한 순서대로 귀납법을 실시한다고 생각해 봅시다.

처음의 정점은 종점 그자체 입니다. \(d_{f'}(t) = d_{f}(t) = 0\)임은 정말로 자명합니다.

이제 임의의 정점 \(v\)에 대해서 생각해 봅시다. 정렬한 결과물을 기준으로 \(v\)보다 앞에 있는 정점들은 귀납법이 증명하고자 하는 가정을 만족시킵니다.(귀납 가정) \(d_{f'}(v)\)가 \(\infin\)인 경우와, \(\infin\)이 아닌 경우로 나누어서 생각해 봅시다. \(d_{f'}(v) = \infin\) 인 경우는 \(d_f(v) \le \infin\)이 매우 자명하므로, 따로 설명할 필요 없습니다.

\(d_{f'}(v) \ne \infin\)인 경우를 생각해 봅시다. 잔여그래프 \(G_{f'}\)에서 \(v\)에서 \(t\)까지 가는 최단경로에서, \(v\)바로 다음에 오는 정점을 \(u\)라고 합시다. 두가지 경우로 나누어서 살펴봅시다.

  1. 증가경로를 찾기 전, 즉 \(G_{f}\)에서 \((v,u)\) 간선이 있었을 경우 :

    \[d_{f'}(v)=d_{f'}(u)+1\ge d_f(u)+1 \ge d_f(v)\]

    가 성립합니다. 첫번째 부등식은 우리의 귀납 가정에 의해서 성립하고, 두번째 부등식은 \((u,v)\)가 \(G_f\)에 있기 떄문에 성립합니다. 따라서 이 경우에는 우리의 추측이 옳음을 알 수 있습니다.

  2. 증가경로를 찾기 전, 즉 \(G_f\)에서 \((v,u)\) 간선이 없었을 경우 : 원래는 \((v,u)\)간선이 없었는데 증가 경로를 찾은 후 \((v,u)\)가 생긴것을 보아, 찾은 증가경로에 \((u,v)\)가 포함되어, \((u,v)\)의 역방향 간선으로 \((v,u)\)가 생겼다고 추론할 수 있습니다. 따라서 \(d_f(u)= d_f(v) + 1\)임을 알 수 있고, 이를 바탕으로 부등식을 작성하면 \(d_{f'}(v)=d_{f'}(u)+1\ge d_f(u)+1 \ge d_f(v) + 2 \ge f(v)\) 임을 확인 할 수 있기 떄문에 이 경우에도 우리의 추측이 맞음을 알 수 있습니다.

이렇게 잔여그래프 위에서의 거리의 증가성에 대해서 증명을 완료했습니다. 이 성질을 활용해서, 다음에 나올 성질을 증명하게 되면, 에드몬즈-카프 알고리즘의 시간 복잡도를 알 수 있게 됩니다.

2. 에드몬즈-카프 알고리즘의 증가경로를 찾는 횟수의 상한

포드-풀커슨 알고리즘의 작동 방식은 증가경로를 더이상 찾지 못할때까지 찾는 것이었고, 증가경로를 적은 횟수로도 찾을 수 있는것을 여러번 찾아서 실행속도가 느릴 수 있다고 서두에 언급하였습니다.

BFS로 증가경로를 찾아내는 에드몬즈-카프 알고리즘은 이런 삽질을 하지 않는다는 것을 보이기 위해서는, 증가경로를 찾는 횟수를 확실히 보이는것처럼 좋은게 없을 것 입니다.

유량 그래프에 흐르는 흐름이 \(f_1\)일때, 이때의 잔여그래프를 \(G_{f_1}\)이라고 합시다. 그리고 \(G_{f_1}\)에서 찾은 증가경로의 병목간선(잔여용량이 가장 작은 간선)을 \((u,v)\)라고 합시다.

\(f_1\) 이후에 또 다시 \((u,v)\)가 병목간선으로 작용할 수 있을까요? \(f_1\)이후에 \((u,v)\)의 역방향 간선인 \((v,u)\)가 병목 간선이 되어(이때의 흐름을 \(f_2\)라고 합시다), 다시 \((u,v)\)가 잔여 그래프에 추가되어 병목 간선이 될 수 있겠지요.

이떄의 상황을 부등식으로 정리하면 아래와 같아집니다.

\[d_{f_3}(u) = d_{f_3}(v) + 1 \ge d_{f_2}(v) + 1 = d_{f_2}(u) +2 \ge d_{f_1}(u) + 2\]

여기서 모든 부등식은 1. 에서 증명했던 잔여 그래프 위에서의 거리의 증가성으로 얻을 수 있습니다.

이 부등식을 보고 알 수 있는 것은, 한 간선이 병목간선으로 작용하고, 또 다시 병목간선이 되려면, 간선에 달려있는 정점의 거리가 적어도 2만큼 늘어난다는 것입니다.

BFS로 증가경로를 찾는 에드몬즈-카프 알고리즘의 특성상, 한 정점에서 가질수 있는 최대의 거리는, 정점의 개수\(\|V\|\) 입니다. 따라서, 한 간선이 병목간선으로 작용할 수 있는 최대의 횟수는 아무리 많아봐야 \(\|V\|/2\)입니다.

에드몬즈-카프 알고리즘으로 증가경로를 찾을 때, 잔여 그래프에서 나올 수 있는 간선의 종류는 원래 그래프에 있었던 정방향 간선과, 그 정방향 간선에 각각 1대1로 대응하는 역방향 간선이기에, 최대로 나올 수 있는 간선의 개수는 \(2\|E\|\)가 됩니다.

한번 증가경로를 찾을 때, 꼭 하나의 병목 간선이 있으므로, 에드몬즈-카프 알고리즘이 증가경로를 찾는 횟수는 \(O(\|V\|\|E\|)\)임을 알 수 있습니다.

에드몬즈-카프 알고리즘의 시간복잡도

증가경로를 찾기 위해 BFS를 한번 수행하는데에 걸리는 시간은 \(O(\|E\|)\)입니다. 위에서 찾은 에드몬즈-카프 알고리즘의 증가경로를 찾는 횟수를 생각하면, 에드몬즈-카프 알고리즘의 시간복잡도는 \(O(\|E\|^2\|V\|)\)가 됩니다.

에드몬즈-카프 알고리즘의 구현(인접행렬)

잔여용량이 남은 간선들만을 이용해서 BFS를 반복적으로 수행하고, 찾은 경로들에게 유량을 보내고, 더이상 할 수 없을때까지 보낸 총 유량을 반환하기만 하면 됩니다.

이하는 c++ 구현입니다.

const int INF = 987654321;
int V;

int capacity[MAX_V][MAX_V], flow[MAX_V][MAX_V];

int networkFlow(int source, int sink){
    memset(flow,0,sizeof(flow));
    int totalFlow = 0;
    while(true){
        vector<int> parent(MAX_V.-1);
        queue<int> q;
        parent[source] = source;
        q.push(source);
        while(!q.empty() && parent[sink] == -1){
            int here = q.front(); q.pop();
            for(int there = 0; there < V; ++there)
                if(capacity[here][there] - flow[here][there] > 0 &&
                    parent[there] == -1){
                    q.push(there);
                    parent[there] = here;
                }
        }
        if(parent[sink] == -1) break;//증가경로가 없으면 종료
        int amount = INF;
        for(int p = sink; p != source; p = parent[p])//병목간선을 찾음
            amount = min(capacity[parent[p]][p] - flow(flow[parent[p]][p], amount);
        for(int p = sink; p != source; p = parent[p]){
            flow[parent[p]][p] += amount;
            flow[p][parent[p]] -= amount;
        }
        totalFlow += amount;
    }
    return totalFlow;
}

구현시 유의사항(인접리스트)

이제 에드몬즈-카프 알고리즘의 시간복잡도를 알게 되어, 상당히 효율적으로 동작한다는 사실을 알게 되었습니다. 우리가 유량 그래프를 사용해서 문제를 풀 때, 인접행렬 뿐만 아니라, 인접 리스트 형태로 그래프를 표현할 떄가 있는데, 이때 알고리즘의 속도를 늦추지 않기 위해서 유의해야할 간단한 사항이 있습니다.

포드-풀커슨 알고리즘의 특성상, 경로에서 찾은 간선으로만 유량을 보내는 것이 아니라, 해당 간선의 반대방향으로도 유량을 보냅니다. 인접행렬로 구현할때는, \(O(1)\)의 속도로 반대편에 바로 접근할 수 있었는데, 인접리스트에서도 \(O(1)\)에 반대편 간선에 접근하여야지 위와 비슷한 속도가 나오겠지요? 그러므로, 간선을 저장하는 구조체에 반대편 간선의 정보도 저장하여, 관리를 한다면 속도를 늦추지 않고 알고리즘을 실행할 수 있을 것입니다.

이하는 위의 사항을 반영한 c++ 코드 구현입니다.

struct Edge{
    int target, capacity, flow;
    Edge* reverse;//역방향 간선
    int residualCapacity() const {return capacity - flow;}
    void push(int amt){
        flow += amt;
        reverse->flow -= amt;
    }
};

vector<Edge*> adj[MAX_V];

void addEdge(int u, int v, int capacity){
    Edge* uv = new Edge(), *vu = new Edge();
    uv->target = v;
    uv->capacity = capacity;
    uv->flow = 0;
    uv->reverse = vu;

    vu->target = u;
    vu->capacity = 0;
    vu->flow = 0;
    vu->reverse = uv;
    adj[u].push_back(uv);
    adj[v].push_back(vu);
}

마무리

이번 글에서는, 포드-풀커슨 방법의 약점이라고 할 수 있는, 증가경로 찾기의 비효율성을 극복하는 에드몬드-카프 알고리즘의 시간복잡도와, 그 구현에 대해서 살펴보았습니다. 다음 글에서는 이 유량 그래프와 최소 컷을 통해서 그래프와는 별 상관 없어 보이는 문제들을 유량 그래프 모델을 통해서 해결할 수 있는지 알아보도록 하겠습니다. 끝까지 읽어주셔서 감사합니다.

참고한 글